Блиц-тур для школ. Примеры заданий
1. Непредельная кислота A – участник цикла Кребса. Геометрический изомер A – малеиновая кислота. Сколько граммов яблочной кислоты теоретически можно получить при гидратации 58 г A? Ответ представьте в виде целого числа без размерности.
2. Любопытные студенты-физики, со склонностью к математике, соединили 12 одинаковых конденсаторов так, что получился октаэдр. Емкость каждого конденсатора равна C. Студентов заинтересовал вопрос, чему равна емкость получившейся цепи между двумя смежными узлами. Помогите им, определив эту емкость в единицах C с точностью до первого десятичного знака.
3. Какой вывод будет иметь программа?
include <stdio.h>
int main() {
int val[10] = 0, 0, 0, 0, 0, 0, 0, 0, 0, 0;
int sum = 0;
int i;
for( val[4] = 0; val[4] < 10; val[4]++) {
val[val[4]] = val[4] * 2;
}
for( i = 0; i < 10; i++) {
sum = sum + val[i];
}
printf( %d, sum);
}
4. Спортсмена сфотографировали с расстояния 20 м камерой с фокусным расстоянием 45 мм. На снимке изображение оказалось смазанным, размазка составила 1 мм. Время экспозиции составило 0.02 c. С какой скоростью двигался спортсмен перпендикулярно главной оптической оси линзы?
5. Четыре бегуна A, B, C и D будут бежать по стадиону, на котором есть 20 параллельных дорожек, пронумерованных от 1 до 20. Организаторы забега называют распределение бегунов по дорожкам оптимальным, если между каждой парой бегунов есть по крайней мере 3 пустые дорожки, т. е. если два бегуна бегут по дорожкам с номерами i и j, то |i − j| ≥ 4. (Например, распределение дорожек 15, 1, 5, 20 бегунам A, B, C, D соответственно является оптимальным.) Сколько существует оптимальных распределений бегунов?
6. На встречу выпускников пришло несколько человек, и каждый из них пожал каждому руку. Всего было совершено 435 рукопожатий. Сколько людей пришло на встречу?
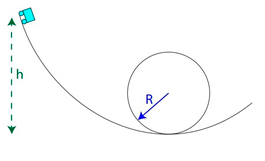
7. Тележка американской горки начинает движение из состояния покоя на высоте h над землей и по пути описывает мертвую петлю. Определите минимальную высоту h в единицах радиуса петли R, так чтобы тележка не отрывалась от направляющих во время прохождения петли. Трением пренебречь.
8. Вычислите определенный интеграл
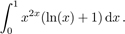
(Здесь ln(x) — это натуральный логарифм.)
9. В пространстве даны 24 точки, никакие три из которых не лежат на одной прямой. Отмечены все плоскости, которые содержат хотя бы три данные точки. Укажите наибольшее возможное количество отмеченных плоскостей, если известно, что их отмечено не более 2017.
10. Сколько существует целых чисел a, для которых уравнение 2x3+x2−20x+a = 0 имеет ровно 3 различных действительных корня?
11. Сплав меди и цинка имеет кубическую гранецентрированную решетку. В элементарной ячейке все вершины заняты атомами цинка, а центры всех граней – атомами меди. Сколько атомов меди приходится на один атом цинка в этом сплаве? Ответ дайте в виде натурального числа.
12. В правом кармане Гирая лежали три банкноты по 100 лир и две по 50 лир; в левом – четыре банкноты по 50 лир и две по 100 лир. Гирай переложил случайную банкноту из левого кармана в правый, а потом случайную банкноту из правого кармана в левый. После этого из его правого кармана украли случайную банкноту. Во сколько раз вероятность того, что была украдена банкнота в 100 лир, больше вероятности того, что была украдена банкнота в 50 лир?
Другие задачи и результаты ответов можно посмотреть на сайте олимпиады